Interval Of Convergence For Taylor Series
Muz Play
Mar 27, 2025 · 5 min read
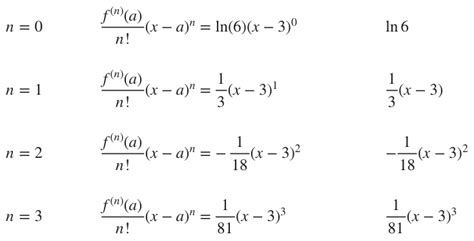
Table of Contents
Interval of Convergence for Taylor Series: A Comprehensive Guide
The Taylor series, a powerful tool in calculus and analysis, allows us to represent a function as an infinite sum of terms. Understanding the interval of convergence is crucial because it dictates where this representation is valid. Outside this interval, the series may diverge, rendering it useless for approximating the function's value. This article delves into the intricacies of determining the interval of convergence for Taylor series, exploring various methods and providing practical examples.
What is a Taylor Series?
Before diving into the interval of convergence, let's refresh our understanding of Taylor series. Given a function f(x) that possesses derivatives of all orders at a point a, its Taylor series expansion around a is given by:
f(x) = Σ [f⁽ⁿ⁾(a) / n!] * (x - a)ⁿ, where n ranges from 0 to ∞
Here:
- f⁽ⁿ⁾(a) represents the nth derivative of f(x) evaluated at x = a.
- n! is the factorial of n.
- (x - a)ⁿ is the nth power of (x - a).
The Taylor series attempts to approximate the function f(x) using an infinite sum of terms. The accuracy of this approximation depends heavily on the value of x and the convergence of the series.
The Importance of the Interval of Convergence
The interval of convergence is the range of x values for which the Taylor series converges to the function f(x). Outside this interval, the series may diverge, meaning the sum of its terms doesn't approach a finite limit. This divergence renders the Taylor series useless for approximating f(x) in those regions. Therefore, identifying the interval of convergence is crucial for correctly applying and interpreting the Taylor series representation.
Determining the Interval of Convergence: The Ratio Test
One of the most common methods for finding the interval of convergence is the ratio test. This test examines the limit of the ratio of consecutive terms in the series. If this limit is less than 1, the series converges absolutely.
Steps using the Ratio Test:
-
Write out the general term: Identify the general term, aₙ, of the Taylor series. This is the nth term in the infinite sum.
-
Calculate the ratio |aₙ₊₁ / aₙ|: Determine the absolute value of the ratio of the (n+1)th term to the nth term.
-
Evaluate the limit: Compute the limit of this ratio as n approaches infinity:
L = lim (n→∞) |aₙ₊₁ / aₙ| -
Interpret the result:
- L < 1: The series converges absolutely.
- L > 1: The series diverges.
- L = 1: The test is inconclusive; other tests are needed.
-
Determine the endpoints: Once you've found the values of x for which L < 1, you need to separately check the convergence at the endpoints of the interval. This often involves using other convergence tests like the alternating series test or the p-series test.
Example: Finding the Interval of Convergence using the Ratio Test
Let's find the interval of convergence for the Taylor series of f(x) = eˣ around a = 0 (the Maclaurin series):
The Maclaurin series for eˣ is:
eˣ = Σ (xⁿ / n!), where n ranges from 0 to ∞
-
General term: aₙ = xⁿ / n!
-
Ratio:
|aₙ₊₁ / aₙ| = |(xⁿ⁺¹ / (n+1)!) / (xⁿ / n!)| = |x| / (n + 1) -
Limit:
L = lim (n→∞) |x| / (n + 1) = 0 -
Interpretation: Since L = 0 < 1 for all x, the series converges absolutely for all real numbers. Therefore, the interval of convergence is (-∞, ∞). No need to check endpoints as the series converges everywhere.
Other Convergence Tests
While the ratio test is widely used, it's not always conclusive. Other tests can be employed to determine convergence at the endpoints or when the ratio test yields L = 1:
-
Root Test: Similar to the ratio test, but examines the nth root of the absolute value of the terms.
-
Alternating Series Test: Applicable to alternating series (where terms alternate in sign). Convergence is guaranteed if the absolute values of the terms decrease monotonically to zero.
-
Comparison Test: Compares the series to another series whose convergence is known.
-
Limit Comparison Test: A variation of the comparison test that uses limits to compare series.
-
Integral Test: Relates the convergence of a series to the convergence of an integral.
Radius of Convergence
Closely related to the interval of convergence is the radius of convergence, denoted by R. It represents half the length of the interval of convergence. If the interval is (-∞, ∞), the radius is considered to be ∞. For an interval (a - R, a + R), the series converges for all x values within this distance from the center of expansion, a.
The radius of convergence often plays a vital role in determining the interval of convergence, particularly when working with power series (a specific case of Taylor series).
Applications of Interval of Convergence
Understanding the interval of convergence is vital in numerous applications:
-
Approximations: Taylor series are frequently used to approximate function values, particularly when evaluating complex functions or when dealing with transcendental numbers (like e or π). Knowing the interval of convergence helps determine the accuracy of these approximations.
-
Solving Differential Equations: Taylor series expansions can be used to find approximate solutions to differential equations, especially those that lack closed-form solutions. The interval of convergence helps in assessing the validity of these solutions.
-
Numerical Analysis: Many numerical methods rely on approximating functions or integrals. Taylor series play a crucial role in developing these methods, and the interval of convergence directly impacts the reliability and accuracy of the results.
Advanced Topics
The concept of interval of convergence extends to more complex scenarios:
-
Complex Analysis: Taylor series can be extended to complex functions, leading to intriguing results regarding regions of convergence in the complex plane.
-
Laurent Series: For functions with singularities, Laurent series provide a more generalized approach, encompassing the Taylor series as a specific case. Understanding the annulus of convergence is crucial for Laurent series.
Conclusion
The interval of convergence is an essential aspect of understanding and utilizing Taylor series effectively. By mastering the techniques presented in this article, including the ratio test, alternative convergence tests, and understanding of the radius of convergence, you can confidently determine the range of x values where Taylor series accurately represents a function, leading to more robust applications in various fields. Remember to always check the endpoints separately, as convergence at the boundary can be tricky to assess. The more you practice applying these concepts, the more intuitive it will become.
Latest Posts
Latest Posts
-
What Does The Nernst Equation Tell Us
Mar 30, 2025
-
What Are The Characteristics Of A Solid
Mar 30, 2025
-
What Is The Difference Between Empirical Formula And Molecular Formula
Mar 30, 2025
-
What Is The Function Of A State
Mar 30, 2025
-
How Are Vestigial Structures An Example Of Evidence Of Evolution
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Interval Of Convergence For Taylor Series . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
