Principle Of Conservation Of Angular Momentum
Muz Play
Mar 31, 2025 · 7 min read
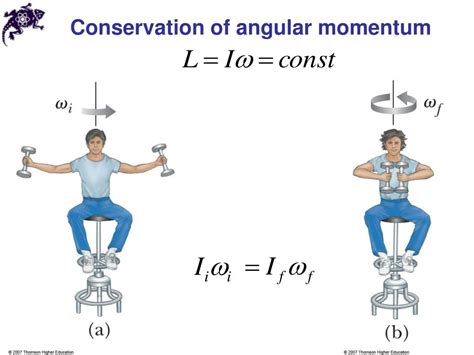
Table of Contents
The Principle of Conservation of Angular Momentum: A Deep Dive
The principle of conservation of angular momentum is a fundamental law in physics, governing the rotation of objects. It's a cornerstone of understanding everything from the spin of electrons to the rotation of galaxies. This principle states that the total angular momentum of a closed system remains constant in the absence of external torques. This seemingly simple statement has profound implications across various fields of science. Let's delve deeper into this crucial principle, exploring its definition, applications, and significance.
Understanding Angular Momentum: More Than Just Rotation
Before we dive into the conservation principle, let's first understand what angular momentum actually is. It's not simply a measure of how fast something is spinning; it's a more nuanced concept that incorporates both the mass distribution and the rotation rate of an object. Formally, angular momentum (L) is defined as:
L = Iω
Where:
- L represents angular momentum (measured in kg⋅m²/s)
- I represents the moment of inertia (kg⋅m²) – a measure of how difficult it is to change an object's rotation. It depends on the object's mass and how that mass is distributed relative to the axis of rotation. A larger moment of inertia indicates a greater resistance to changes in rotational motion.
- ω represents angular velocity (rad/s) – a measure of how fast the object is rotating.
Think of it this way: a figure skater spinning with their arms outstretched has a certain angular momentum. When they pull their arms in, their moment of inertia decreases (mass is closer to the axis of rotation), and to conserve angular momentum, their angular velocity must increase – they spin faster. This is a classic demonstration of the principle in action.
Moment of Inertia: A Closer Look
The moment of inertia is a crucial component in understanding angular momentum. It's not simply the mass; it's how the mass is distributed. Consider these examples:
- A solid sphere: A solid sphere rotating about its diameter has a lower moment of inertia compared to a hollow sphere of the same mass and radius. This is because the mass in the solid sphere is more concentrated towards the axis of rotation.
- A rod: The moment of inertia of a rod rotating about its center is different than if it rotates about one end. In the latter case, the moment of inertia is greater because the mass is further from the axis of rotation.
- Complex shapes: Calculating the moment of inertia for complex shapes can be challenging and often requires integral calculus. However, for many standard shapes, the formulas are readily available.
Understanding the moment of inertia is crucial for predicting how an object's rotation will change in response to external forces or internal mass redistribution.
The Conservation Principle: A Timeless Law
The principle of conservation of angular momentum states that the total angular momentum of a closed system remains constant if no external torque acts on the system. A closed system is one that doesn't interact with its surroundings – no external forces or torques are applied. This principle is a direct consequence of Newton's laws of motion and is a fundamental symmetry of the universe.
Mathematically, the conservation principle can be expressed as:
ΔL = 0 (or Lᵢ = Lƒ)
Where:
- ΔL represents the change in angular momentum.
- Lᵢ represents the initial angular momentum.
- Lƒ represents the final angular momentum.
This means that if the angular momentum of a system changes, it must be due to an external torque acting upon it. The absence of an external torque implies a constant angular momentum.
Real-World Applications: From Figure Skating to Galaxies
The principle of conservation of angular momentum manifests itself in a wide array of phenomena, from everyday occurrences to cosmological events:
1. Figure Skating and Diving:
As mentioned earlier, figure skaters and divers utilize this principle to control their rotation. By pulling their limbs closer to their body, they reduce their moment of inertia and increase their angular velocity, resulting in faster spins. Conversely, extending their limbs increases their moment of inertia and slows their rotation.
2. Rotating Machinery:
In engineering, the principle is crucial in designing rotating machinery like turbines, gyroscopes, and flywheels. The design of these systems must account for the conservation of angular momentum to ensure stable and predictable operation. Gyroscopes, for example, maintain their orientation due to their conserved angular momentum.
3. Planetary Motion:
The conservation of angular momentum plays a vital role in understanding the motion of planets around the sun. As planets orbit, their distance from the sun may vary slightly, but their angular momentum remains essentially constant. This is why planets move faster when closer to the sun and slower when farther away. Kepler's second law of planetary motion is a direct consequence of this principle.
4. Neutron Stars and Pulsars:
Neutron stars are incredibly dense remnants of massive stars. During their formation, they conserve angular momentum, resulting in extremely rapid rotation. Some neutron stars, known as pulsars, emit beams of radiation that sweep across the sky, appearing as pulses, due to their rapid rotation.
5. Galaxies and Galactic Rotation Curves:
The rotation of galaxies is another fascinating example. The observation of galactic rotation curves – the speed of stars orbiting the galactic center as a function of their distance – provides strong evidence for the existence of dark matter. The observed rotation speeds are much faster than predicted by the visible matter alone, suggesting the presence of a significant amount of unseen mass contributing to the galaxy's angular momentum.
6. The Earth's Rotation:
The Earth's rotation itself is governed by the principle of conservation of angular momentum. While tidal forces from the moon cause a gradual slowing of Earth's rotation, the overall angular momentum is still largely conserved over shorter timescales.
7. Atomic and Subatomic Physics:
At the quantum level, the principle of conservation of angular momentum is essential in understanding the behavior of electrons in atoms and the properties of subatomic particles. The spin of electrons, for instance, is a form of intrinsic angular momentum.
When Conservation Doesn't Hold: External Torques
It's crucial to remember that the principle of conservation of angular momentum only applies when there are no external torques acting on the system. If an external torque is present, the angular momentum of the system will change.
Examples of external torques include:
- Frictional forces: Friction acts as an external torque that slows down rotating objects, reducing their angular momentum.
- Gravitational forces: In some situations, gravitational forces can exert a torque on a rotating object, altering its angular momentum.
- Magnetic forces: Magnetic fields can exert torques on objects with magnetic moments, changing their angular momentum.
In these scenarios, the change in angular momentum is directly related to the magnitude and duration of the external torque.
Conclusion: A Universal Principle with Far-Reaching Consequences
The principle of conservation of angular momentum is a powerful and far-reaching concept in physics. Its implications extend from the macroscopic world of planets and galaxies to the microscopic world of atoms and subatomic particles. Understanding this principle is crucial for comprehending a wide range of physical phenomena and for developing technologies that utilize rotational motion. The seemingly simple equation, L = Iω, unlocks a vast understanding of the universe's fundamental workings, showcasing the elegance and power of conservation laws in physics. Further exploration into the intricacies of moment of inertia and the effects of external torques allows for a more profound appreciation of this fundamental principle and its ubiquitous presence in the physical world. The seemingly simple act of a figure skater spinning elegantly illustrates the profound implications of this powerful law of physics, a law that governs the rotation of everything from subatomic particles to celestial bodies.
Latest Posts
Latest Posts
-
How Do You Find The Boiling Point Of A Solution
Apr 02, 2025
-
What Happens To Ionization Energy Down A Group
Apr 02, 2025
-
How Many Grams In A Molecule
Apr 02, 2025
-
Is Cl A Metal Or Nonmetal
Apr 02, 2025
-
Microscopic Anatomy And Organization Of Skeletal Muscle
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Principle Of Conservation Of Angular Momentum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
