What Is Periodic Motion In Physics
Muz Play
Mar 27, 2025 · 6 min read
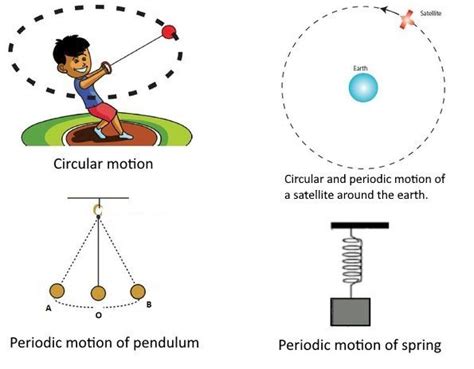
Table of Contents
What is Periodic Motion in Physics? A Comprehensive Guide
Periodic motion, a fundamental concept in physics, describes the repetitive movement of an object or system about a central point or equilibrium position. Understanding periodic motion is crucial for comprehending a wide range of phenomena, from the swing of a pendulum to the vibrations of atoms in a solid. This comprehensive guide will delve into the intricacies of periodic motion, exploring its defining characteristics, different types, and practical applications.
Defining Periodic Motion: Key Characteristics
At the heart of periodic motion lies repetition. This means the motion repeats itself after a fixed time interval, known as the period (T). Another crucial characteristic is the frequency (f), which represents the number of complete cycles or oscillations the object undergoes per unit of time. Frequency and period are inversely related: f = 1/T. The units for frequency are Hertz (Hz), representing cycles per second.
Beyond repetition and defined frequency, periodic motion often involves a restoring force. This force consistently acts to pull the object back towards its equilibrium position. The strength of this force is often proportional to the displacement from equilibrium, a key feature of simple harmonic motion (SHM), a special case of periodic motion that we will explore in detail later.
Types of Periodic Motion
The world of periodic motion is diverse, encompassing various types of repetitive movements. Here are some prominent examples:
1. Simple Harmonic Motion (SHM)
Simple harmonic motion is arguably the most fundamental type of periodic motion. It's characterized by a restoring force directly proportional to the displacement from equilibrium and directed towards the equilibrium position. Mathematically, this relationship is represented by:
F = -kx
Where:
- F is the restoring force
- k is the spring constant (a measure of the stiffness of the system)
- x is the displacement from equilibrium
Many systems exhibit SHM, including:
- Mass-spring system: A mass attached to a spring oscillates back and forth.
- Simple pendulum: A mass suspended from a string swings back and forth in a small angle approximation.
- LC circuit: In an electrical circuit containing an inductor (L) and a capacitor (C), the charge oscillates periodically.
The motion in SHM can be described using sinusoidal functions (sine and cosine) with a specific period and amplitude. The amplitude represents the maximum displacement from the equilibrium position.
2. Damped Oscillations
In real-world scenarios, periodic motion is often affected by damping forces. These forces, such as friction or air resistance, oppose the motion and gradually reduce the amplitude of oscillations over time. The rate at which the amplitude decays depends on the strength of the damping force. Different levels of damping lead to:
- Underdamped oscillations: The oscillations gradually decrease in amplitude until they eventually stop.
- Critically damped oscillations: The system returns to equilibrium as quickly as possible without oscillating.
- Overdamped oscillations: The system returns to equilibrium slowly without oscillating.
3. Driven Oscillations and Resonance
When a periodic external force is applied to an oscillating system, it leads to driven oscillations. The frequency of the external force is crucial. If the frequency of the driving force matches the natural frequency of the system (its frequency of oscillation without any external force), resonance occurs. Resonance leads to a significant increase in the amplitude of oscillations, potentially causing damage or destruction if not carefully managed. Examples include:
- Swinging a child on a swing: Pushing at the right frequency maximizes the swing's amplitude.
- Shattering a wine glass with sound: A sound wave at the glass's natural frequency can cause it to vibrate with such a large amplitude that it shatters.
4. Coupled Oscillations
When two or more oscillating systems interact, they exhibit coupled oscillations. The interaction can lead to complex patterns of motion, with energy exchanged between the systems. Examples include:
- Two coupled pendulums: The pendulums' swings influence each other.
- Molecular vibrations: Atoms in a molecule vibrate and interact with each other.
5. Anharmonic Oscillations
While SHM is characterized by a restoring force directly proportional to displacement, many real-world systems exhibit anharmonic oscillations. This means the restoring force is not linearly proportional to displacement. Anharmonic oscillations often involve more complex mathematical descriptions, and their periods might not be constant. Examples include:
- Pendulum with large angles: The pendulum's period depends on the amplitude of swing.
- Molecular vibrations at high energies: The restoring forces deviate from linearity.
Mathematical Description of Periodic Motion
The mathematical description of periodic motion relies heavily on trigonometric functions. For SHM, the displacement (x) as a function of time (t) can be represented as:
x(t) = A cos(ωt + φ)
Where:
- A is the amplitude
- ω is the angular frequency (ω = 2πf = 2π/T)
- φ is the phase constant (determines the initial position)
Velocity and acceleration can be derived by taking the first and second derivatives of the displacement equation, respectively. These equations provide a complete mathematical description of the motion.
Applications of Periodic Motion
Periodic motion's significance extends far beyond theoretical physics. Its principles are applied extensively in various fields:
- Clocks and watches: The oscillatory motion of pendulums or balance wheels provides the timekeeping mechanism.
- Musical instruments: The vibrations of strings, air columns, or membranes produce musical sounds.
- Electronics: LC circuits in radios and other electronic devices rely on periodic oscillations.
- Medical imaging: Techniques like MRI use the principles of nuclear magnetic resonance, which is a type of periodic motion.
- Structural engineering: Understanding periodic motion is essential for designing buildings and bridges that can withstand vibrations from earthquakes or wind.
- Quantum mechanics: The periodic motion of electrons in atoms underlies the properties of matter.
Advanced Topics in Periodic Motion
Beyond the basics, several advanced topics delve deeper into the intricacies of periodic motion:
- Nonlinear oscillations: These oscillations involve systems where the restoring force is not linearly proportional to displacement. They can exhibit chaotic behavior.
- Chaos theory: This field explores the complex and unpredictable behavior of nonlinear dynamical systems, including many oscillatory systems.
- Fourier analysis: This powerful mathematical technique allows decomposition of complex periodic motions into simpler sinusoidal components.
Conclusion
Periodic motion is a fundamental concept with profound implications across numerous scientific and engineering disciplines. From the simple swing of a pendulum to the complex vibrations of molecules, understanding periodic motion provides a framework for comprehending the world around us. Its mathematical description, diverse types, and broad range of applications make it a cornerstone of physics and a subject worthy of continued exploration. The concepts presented here provide a solid foundation for further study into this fascinating area of physics. By understanding the principles of periodic motion, you gain valuable insights into the behavior of numerous physical systems and open doors to more advanced concepts in physics and beyond.
Latest Posts
Latest Posts
-
Duties Of An Agent In Law
Mar 30, 2025
-
What Is The Symbol For Population Variance
Mar 30, 2025
-
Adding Rational Expressions With Unlike Denominators
Mar 30, 2025
-
Where Protons And Neutrons Are Located
Mar 30, 2025
-
How To Find The Extinction Coefficient
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about What Is Periodic Motion In Physics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
