What Is The Tension In The Rope
Muz Play
Apr 02, 2025 · 6 min read
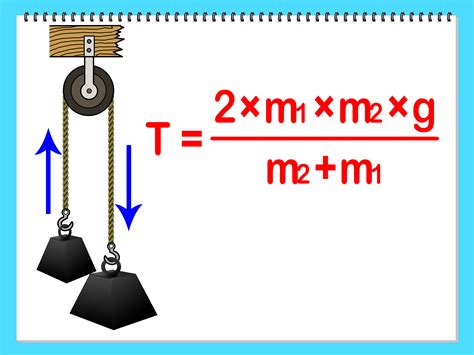
Table of Contents
What is the Tension in the Rope? A Deep Dive into Statics and Dynamics
Understanding tension in a rope is fundamental to various fields, from basic physics to advanced engineering. This seemingly simple concept hides a rich tapestry of physical principles and mathematical applications. This article will explore the concept of rope tension in detail, covering both static and dynamic scenarios, and delving into the factors that influence it. We’ll examine various scenarios, from simple systems to more complex configurations, providing a comprehensive understanding of this crucial concept.
Understanding Tension: A Fundamental Force
Tension, in the context of a rope or cable, is the pulling force transmitted axially through the rope. It's a force that acts along the length of the rope, pulling equally in opposite directions. Imagine pulling on both ends of a taut rope. The tension is the magnitude of that pulling force at any point along the rope. Crucially, this force is internal to the rope; it's the force that the rope exerts on itself.
It’s important to differentiate tension from compression. While tension involves pulling forces, compression involves pushing forces. A rope under tension will stretch slightly, while a column under compression will shorten. This difference in behavior is key to understanding how ropes and cables are used in structural applications.
Static Tension: The Rope at Rest
When a rope is at rest, the forces acting upon it are balanced. This is the realm of statics, a branch of mechanics dealing with bodies at rest or in uniform motion. Consider a simple scenario: a weight hanging from a rope attached to a ceiling. The weight exerts a downward force (gravity), and the rope exerts an upward force (tension) to counteract it. In this equilibrium state, the tension in the rope is equal to the weight of the object.
Factors influencing static tension:
- Weight of the object: The heavier the object, the greater the tension in the rope. This is a direct proportionality.
- Angle of the rope: If the rope is not perfectly vertical (e.g., a weight suspended from two ropes at an angle), the tension in each rope will be greater than the weight. This is because the tension components must resolve vertically to balance the weight and horizontally to cancel each other out.
- Friction: If there's friction between the rope and any surface it touches (e.g., a pulley), it will affect the tension. Friction will generally increase the tension required to maintain equilibrium.
Calculating Static Tension:
Calculating static tension often involves resolving forces using vector diagrams and applying Newton's first law of motion (a body at rest remains at rest unless acted upon by an external force). For simple systems, this is relatively straightforward. However, more complex systems, especially those with multiple ropes and angles, might require more advanced methods such as free-body diagrams and simultaneous equations.
Dynamic Tension: The Rope in Motion
When a rope is in motion, the situation becomes more complex. This is the domain of dynamics, where the forces acting on the rope and its subsequent acceleration are considered. Dynamic tension involves inertia, momentum, and changing forces over time.
Factors influencing dynamic tension:
- Mass of the rope: A heavier rope will require more force to accelerate, increasing the tension. We can no longer simply ignore the mass of the rope itself as we did in static scenarios.
- Acceleration: The greater the acceleration of the system, the greater the tension. If you accelerate an object upwards on a rope, the tension will be greater than the object’s weight.
- Jerk: Sudden changes in acceleration (jerk) can create significant peaks in tension, potentially leading to rope failure.
- Wave propagation: In a long, flexible rope, waves can propagate along its length. The tension influences the speed of these waves.
Calculating Dynamic Tension:
Calculating dynamic tension requires applying Newton's second law of motion (F = ma), where 'F' is the net force acting on the system, 'm' is the mass, and 'a' is the acceleration. For simple systems, this can be relatively straightforward. However, more complex systems, such as those involving swinging pendulums or waves on a rope, may require more sophisticated mathematical tools like differential equations.
Real-World Applications of Tension in Ropes
The concept of tension in ropes has widespread practical applications across various fields. Let’s explore a few examples:
1. Construction and Engineering
Tension is crucial in many construction and engineering applications. Consider suspension bridges, where massive cables are under immense tension to support the bridge deck. The design and engineering of these cables require precise calculations to ensure that the tension is distributed evenly and within the strength limits of the material. Similarly, cranes and lifting equipment rely on the principles of tension to safely lift heavy loads.
2. Sports and Recreation
Many sports involve ropes under tension. Consider rock climbing, where the rope must withstand substantial tension to prevent a fall. The strength and elasticity of the rope are critical factors here. Similar principles apply to activities like zip-lining, where the cable's tension is vital for safety and controlled descent.
3. Transportation and Logistics
Tension plays a significant role in various aspects of transportation and logistics. Consider towing vehicles, where the tow rope is under tension to pull the vehicle. The strength of the rope must be sufficient to handle the weight and forces involved. Similarly, conveyor belts rely on tension to maintain their operation, transporting goods efficiently.
4. Medical Applications
Tension in ropes and cables is utilized in several medical applications, notably in orthopedic surgery and rehabilitation. Certain surgical procedures use specialized cables and ropes to stabilize bones and joints, relying on precise tension control for optimal healing.
Advanced Concepts and Considerations
The understanding of rope tension can be further deepened by considering more advanced concepts:
- Rope Elasticity: Real ropes are not perfectly inelastic. They stretch under tension, and this elasticity affects the tension distribution and the overall system behavior. Hooke's Law (stress is proportional to strain within the elastic limit) is relevant here.
- Rope Material Properties: Different rope materials (nylon, steel, etc.) have different tensile strengths, elasticity, and other properties that influence their behavior under tension.
- Multiple-Rope Systems: Systems with multiple ropes and pulleys introduce more complexities, requiring advanced vector analysis and consideration of friction and pulley efficiency.
- Dynamic Loading and Shock Absorption: Sudden changes in load or impact can lead to significant spikes in tension, potentially exceeding the rope's breaking strength. Understanding these dynamic loading scenarios is critical for safety.
- Failure Analysis: Predicting when a rope will fail under tension requires understanding its material properties, the load it carries, and the environmental conditions it's subjected to. Factor of safety is a critical design parameter.
Conclusion
The tension in a rope is a fundamental concept with far-reaching implications across various fields. This article has provided a comprehensive overview of this concept, covering both static and dynamic scenarios, and exploring the many factors that influence it. From simple systems to complex engineering structures, a thorough understanding of rope tension is paramount for ensuring safety, efficiency, and proper design. By applying the principles outlined here, engineers, designers, and anyone working with ropes can better predict and control the forces at play, leading to more robust and reliable systems. Remember that careful consideration of all factors, from the weight of the object to the material properties of the rope itself, is crucial for accurate calculations and safe operation.
Latest Posts
Latest Posts
-
Alkali Metals Alkaline Earth Metals Halogens And Noble Gases
Apr 03, 2025
-
What Determines Primary Structure Of A Protein
Apr 03, 2025
-
Chromosomes Disperse And Are No Longer Visible
Apr 03, 2025
-
Difference Between Molecular Weight And Formula Weight
Apr 03, 2025
-
Each Orbital Can Hold How Many Electrons
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Tension In The Rope . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
