What Is The Unit Of Angular Momentum
Muz Play
Apr 05, 2025 · 6 min read
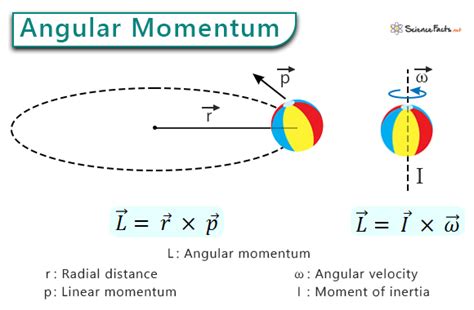
Table of Contents
What is the Unit of Angular Momentum? A Comprehensive Guide
Angular momentum, a crucial concept in physics, describes an object's rotational motion. Understanding its unit is fundamental to grasping its implications in various fields, from celestial mechanics to quantum physics. This comprehensive guide delves deep into the definition, calculation, and significance of the unit of angular momentum. We'll explore its connection to other physical quantities and demonstrate its application through examples.
Defining Angular Momentum
Before diving into the unit, let's establish a clear understanding of angular momentum itself. Angular momentum (often denoted as L) is a vector quantity that represents the rotational equivalent of linear momentum. While linear momentum describes an object's tendency to continue moving in a straight line, angular momentum describes its tendency to continue rotating.
Several factors influence the magnitude of an object's angular momentum:
- Mass (m): A more massive object possesses a greater tendency to resist changes in its rotational motion.
- Velocity (v): The speed of rotation directly impacts angular momentum. Faster rotation implies greater angular momentum. Note that we're referring to tangential velocity here – the velocity perpendicular to the radius of rotation.
- Radius (r): The distance from the axis of rotation also plays a crucial role. An object further from the axis of rotation has greater angular momentum for the same tangential velocity.
For a point mass rotating about a fixed axis, angular momentum is given by the formula:
L = Iω
Where:
- L represents angular momentum
- I represents the moment of inertia (a measure of an object's resistance to changes in its rotation)
- ω represents the angular velocity (the rate of change of angular displacement)
Another way to express angular momentum, particularly useful for understanding its vector nature, is:
L = r x p
Where:
- r is the position vector from the axis of rotation to the object
- p is the linear momentum vector (mass x velocity)
- x denotes the cross product, resulting in a vector perpendicular to both r and p. This perpendicularity demonstrates the direction of the angular momentum vector.
The Unit of Angular Momentum: Kilogram-meter squared per second (kg⋅m²/s)
The unit of angular momentum is derived directly from the fundamental units of mass, length, and time within the International System of Units (SI). Let's break down how:
- Kilogram (kg): Represents the mass (m) of the rotating object.
- Meter squared (m²): Derived from the radius (r) squared (in the
r x pformulation), or the combination of radius and other factors contributing to the moment of inertia (I). This represents the distance from the axis of rotation. - Second (s): Represents the time (implied in angular velocity ω or linear velocity v).
Therefore, the complete unit of angular momentum is kilogram-meter squared per second (kg⋅m²/s). This unit reflects the physical quantities influencing rotational motion: mass, distance, and time.
Understanding the Unit through Dimensional Analysis
Dimensional analysis provides a powerful tool for understanding the unit of angular momentum. It verifies the consistency of the formula and its units. Let's examine the L = Iω and L = r x p formulations:
-
L = Iω: The moment of inertia (I) has units of kg⋅m². Angular velocity (ω) has units of radians/second (rad/s). Radians are dimensionless, so the units of Iω are kg⋅m²/s, confirming our unit for angular momentum.
-
L = r x p: The position vector (r) has units of meters (m). Linear momentum (p) has units of kilogram-meters per second (kg⋅m/s). The cross product of these vectors results in units of kg⋅m²/s, again validating our unit.
Significance of the Unit
The consistency of the unit across different formulations highlights the fundamental nature of angular momentum. The unit itself isn't just an arbitrary label; it encodes the physical meaning and dependencies of this crucial quantity. For example, a larger kg⋅m²/s value indicates a greater resistance to changes in rotational motion, requiring a larger torque to alter it.
Angular Momentum in Different Contexts
The concept of angular momentum and its unit are pivotal across numerous scientific domains:
1. Classical Mechanics:
In classical mechanics, angular momentum is crucial for understanding planetary orbits, the motion of gyroscopes, and the rotation of rigid bodies. The conservation of angular momentum, a fundamental principle, states that in the absence of external torques, the total angular momentum of a system remains constant. This principle governs phenomena like a figure skater's spinning speed increasing as they pull their arms inward, reducing their moment of inertia while conserving angular momentum.
2. Quantum Mechanics:
In quantum mechanics, angular momentum is quantized. This means it can only take on specific discrete values, multiples of the reduced Planck constant (ħ = h/2π, where h is the Planck constant). This quantization plays a critical role in atomic structure, determining the allowed energy levels of electrons and influencing the properties of atoms and molecules. The unit of angular momentum in quantum mechanics remains the same (kg⋅m²/s), although its values are restricted to specific quanta.
3. Astrophysics:
In astrophysics, angular momentum is crucial for understanding the formation and evolution of stars, galaxies, and other celestial bodies. The conservation of angular momentum plays a vital role in the formation of spiral galaxies and the rotation of stars. The immense angular momentum of these celestial objects significantly impacts their structure and behavior.
4. Engineering:
Engineers utilize the concept of angular momentum in designing various systems, from rotating machinery (e.g., turbines, flywheels) to spacecraft attitude control systems. Understanding the angular momentum of these systems is crucial for stability and efficiency.
Practical Examples Illustrating Angular Momentum and its Unit
Let's consider some practical examples to solidify the understanding of angular momentum and its unit:
Example 1: A spinning top:
Imagine a spinning top with a mass of 0.1 kg, a radius of 0.05 meters, and an angular velocity of 10 rad/s. To calculate its angular momentum, we need to approximate its moment of inertia. For a simple top, we can approximate it as a solid cylinder: I ≈ (1/2)mr². Plugging in the values:
I ≈ (1/2) * 0.1 kg * (0.05 m)² ≈ 1.25 x 10⁻⁴ kg⋅m²
L = Iω ≈ 1.25 x 10⁻⁴ kg⋅m² * 10 rad/s ≈ 1.25 x 10⁻³ kg⋅m²/s
This calculation demonstrates the angular momentum of the spinning top, expressed in the standard unit.
Example 2: A rotating planet:
While a planet's angular momentum calculation is far more complex, involving its non-uniform mass distribution and rotation, the underlying unit remains the same. Its immense angular momentum, expressed in kg⋅m²/s, determines its rotational period and stability.
Example 3: An electron orbiting an atom:
In the quantum realm, an electron orbiting an atom possesses angular momentum, quantized in units of ħ (reduced Planck constant). While the unit remains kg⋅m²/s, its value is restricted to specific discrete levels.
Conclusion
The unit of angular momentum, kilogram-meter squared per second (kg⋅m²/s), is not merely a symbolic representation. It encapsulates the fundamental physical quantities influencing rotational motion: mass, distance, and time. Understanding this unit is paramount to grasping the concept of angular momentum and its wide-ranging applications in classical and quantum mechanics, astrophysics, and engineering. The consistency of the unit across different formulations and its application in diverse fields underscores its fundamental importance in physics. From the smallest subatomic particles to the largest celestial bodies, angular momentum plays a pivotal role in shaping the universe as we know it. Its unit serves as a constant reminder of the physical principles that govern the rotation of matter across all scales.
Latest Posts
Latest Posts
-
What Are The Properties Of Solids
Apr 06, 2025
-
Trends In The Periodic Table Answer Key
Apr 06, 2025
-
How Do Intermolecular Forces Affect Viscosity
Apr 06, 2025
-
Protein Separation By Ion Exchange Chromatography
Apr 06, 2025
-
How Do Organic Sedimentary Rocks Form
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Unit Of Angular Momentum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
