Which Describes An Object In Projectile Motion
Muz Play
Apr 05, 2025 · 6 min read
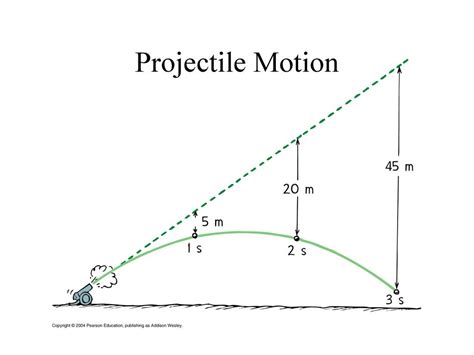
Table of Contents
Decomposing Projectile Motion: A Deep Dive into the Physics of Thrown Objects
Projectile motion is a cornerstone concept in classical mechanics, describing the path of an object launched into the air and subject only to the force of gravity. Understanding projectile motion is crucial in fields ranging from sports science (analyzing a baseball's trajectory) to aerospace engineering (designing missile guidance systems). This article will provide a comprehensive exploration of this fascinating phenomenon, delving into its key components, equations, and practical applications.
Defining Projectile Motion: Key Characteristics
Projectile motion is characterized by several key factors:
-
Negligible Air Resistance: The most fundamental assumption is that air resistance is negligible. While air resistance significantly impacts real-world projectiles, especially at high speeds or over long distances, ignoring it simplifies the analysis and provides a good approximation for many scenarios. We'll initially focus on this idealized case, later addressing how air resistance complicates the picture.
-
Constant Acceleration due to Gravity: The only force acting on the projectile is gravity, resulting in a constant downward acceleration (approximately 9.8 m/s² on Earth). This acceleration is independent of the projectile's mass, velocity, or trajectory.
-
Independent Horizontal and Vertical Motion: The horizontal and vertical components of the projectile's motion are independent of each other. This means that the horizontal velocity remains constant (ignoring air resistance), while the vertical velocity changes uniformly due to gravity. This crucial principle allows us to analyze the motion in two separate dimensions.
Decomposing the Motion: Horizontal and Vertical Components
Analyzing projectile motion involves breaking down the motion into its horizontal and vertical components. This simplifies the problem significantly, allowing us to apply basic kinematic equations independently to each component.
Horizontal Motion (x-component):
-
Constant Velocity: In the absence of air resistance, the horizontal velocity (Vx) remains constant throughout the projectile's flight. This is because there's no horizontal force acting on the object.
-
Equation of Motion: The horizontal displacement (Δx) can be calculated using the simple equation:
Δx = Vx * t
where:
- Δx = horizontal displacement
- Vx = initial horizontal velocity
- t = time
Vertical Motion (y-component):
-
Constant Acceleration: The vertical motion is characterized by constant downward acceleration due to gravity (g ≈ 9.8 m/s²).
-
Equations of Motion: Several kinematic equations govern the vertical motion:
- Vy = Voy - gt (vertical velocity at time t)
- Δy = Voy*t - (1/2)gt² (vertical displacement at time t)
- Vy² = Voy² - 2gΔy (relationship between vertical velocity and displacement)
where:
- Vy = vertical velocity at time t
- Voy = initial vertical velocity
- g = acceleration due to gravity (approximately 9.8 m/s²)
- Δy = vertical displacement
- t = time
Key Parameters and Calculations: Understanding the Trajectory
Several key parameters define the trajectory of a projectile:
-
Initial Velocity (Vo): This is the initial speed at which the projectile is launched. It's often expressed as a magnitude and an angle (θ) above the horizontal.
-
Launch Angle (θ): This angle determines the initial horizontal and vertical components of the velocity. The horizontal component is Vocos(θ), and the vertical component is Vosin(θ).
-
Time of Flight (t): This is the total time the projectile spends in the air. It can be calculated using the vertical motion equations, specifically focusing on when the vertical displacement (Δy) returns to zero (assuming it lands at the same height as it was launched).
-
Range (R): This is the horizontal distance covered by the projectile during its flight. It's calculated using the horizontal displacement equation (Δx) and the time of flight (t).
-
Maximum Height (H): This is the highest point reached by the projectile during its flight. It occurs when the vertical velocity (Vy) becomes zero. This can be calculated using the vertical motion equations.
The Effect of Launch Angle on Trajectory: Optimizing for Range
The launch angle significantly influences the projectile's trajectory and range. For a given initial velocity, there's an optimal launch angle that maximizes the range. In the absence of air resistance, this optimal angle is 45 degrees. At this angle, the horizontal and vertical components of the initial velocity are balanced, leading to the greatest horizontal displacement. Launch angles above or below 45 degrees result in shorter ranges.
Accounting for Air Resistance: A More Realistic Model
The simplified model of projectile motion, neglecting air resistance, provides a good starting point. However, in reality, air resistance plays a significant role, particularly for objects with large surface areas or high speeds. Air resistance is a force that opposes the motion of the object through the air, and its magnitude depends on factors like the object's speed, shape, and the density of the air.
Incorporating air resistance makes the equations of motion much more complex, often requiring numerical methods or computational simulations to solve. The effect of air resistance is to:
- Reduce the horizontal range: Air resistance acts against the horizontal motion, slowing it down and reducing the distance the projectile travels.
- Reduce the maximum height: Air resistance opposes the upward motion, reducing the height the projectile reaches.
- Shorten the time of flight: The projectile will spend less time in the air because air resistance slows both the upward and downward motion.
- Alter the trajectory: The trajectory is no longer a symmetrical parabola but becomes more asymmetrical, with a steeper descent than ascent.
Real-World Applications of Projectile Motion: From Sports to Space Exploration
The principles of projectile motion are applicable across numerous fields:
-
Sports: Analyzing the trajectory of a ball in baseball, basketball, golf, or tennis relies heavily on understanding projectile motion. Factors like launch angle, initial velocity, and spin affect the ball's flight path.
-
Military Applications: Ballistics, the science of projectile motion, is crucial in designing and deploying artillery shells, rockets, and missiles. Precise calculations are essential to ensure accurate targeting.
-
Aerospace Engineering: Understanding projectile motion is fundamental in designing spacecraft trajectories, satellite launches, and the flight paths of aircraft.
-
Civil Engineering: Projectile motion principles are used in designing structures that can withstand impact from objects like falling debris or projectiles.
Conclusion: Beyond the Basics of Projectile Motion
This article has provided a comprehensive overview of projectile motion, starting with its fundamental principles and progressing to more advanced considerations like air resistance. While the simplified model ignoring air resistance offers valuable insights and serves as a strong foundation, it's essential to remember that real-world projectiles are always subject to this complicating factor. The more accurate models, while significantly more complex, are necessary for precise predictions and engineering applications. The power of understanding projectile motion lies in its ability to explain and predict the behavior of objects in motion under the influence of gravity – a phenomenon that's both ubiquitous and profoundly influential in our world. Whether analyzing a soaring basketball or the trajectory of a space probe, the principles discussed here provide a critical framework for understanding this fundamental aspect of physics.
Latest Posts
Latest Posts
-
Give The Iupac Name Of The Branched Alkane
Apr 05, 2025
-
Consider This Step In A Radical Reaction
Apr 05, 2025
-
Cold Temperatures Slow Down The Growth Of Microorganisms
Apr 05, 2025
-
What Happens To Pyruvic Acid During The Krebs Cycle
Apr 05, 2025
-
Co Lewis Structure With Formal Charge
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Describes An Object In Projectile Motion . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
