Acetic Acid Sodium Acetate Buffer Equation
Muz Play
Apr 05, 2025 · 7 min read
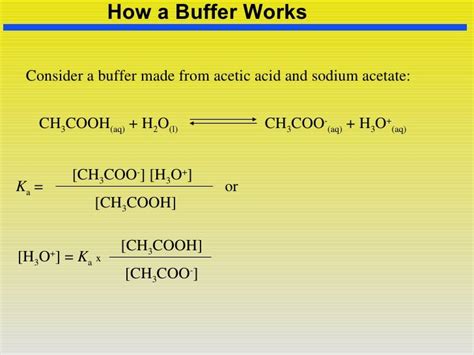
Table of Contents
Acetic Acid Sodium Acetate Buffer: A Comprehensive Guide
The acetic acid sodium acetate buffer system is a classic example of a buffer solution, frequently used in chemistry and biology. Understanding its workings, its equation, and its applications is crucial for many scientific endeavors. This comprehensive guide will delve into the intricacies of this buffer system, explaining its function, the Henderson-Hasselbalch equation's role, practical applications, and considerations for its preparation and use.
What is a Buffer Solution?
Before diving into the specifics of the acetic acid/sodium acetate buffer, let's establish a fundamental understanding of buffer solutions. A buffer solution is an aqueous solution that resists changes in pH upon the addition of small amounts of acid or base. This resistance to pH change is critical in many applications where maintaining a stable pH is essential. Buffers achieve this resistance through the presence of a weak acid and its conjugate base (or a weak base and its conjugate acid).
The Acetic Acid/Sodium Acetate Buffer System
The acetic acid/sodium acetate buffer is comprised of:
- Acetic acid (CH₃COOH): A weak acid that partially dissociates in water, releasing hydronium ions (H₃O⁺).
- Sodium acetate (CH₃COONa): The conjugate base of acetic acid. It dissociates completely in water, providing acetate ions (CH₃COO⁻).
The equilibrium between acetic acid and its conjugate base is the key to the buffer's functionality. The presence of both the weak acid and its conjugate base allows the buffer to neutralize added acids or bases, thus minimizing pH changes.
How it Works: Neutralizing Acids and Bases
-
Adding a strong acid (e.g., HCl): The added H₃O⁺ ions react with the acetate ions (CH₃COO⁻) to form acetic acid (CH₃COOH). This reaction consumes the added H₃O⁺ ions, preventing a significant decrease in pH.
H₃O⁺(aq) + CH₃COO⁻(aq) ⇌ CH₃COOH(aq) + H₂O(l) -
Adding a strong base (e.g., NaOH): The added hydroxide ions (OH⁻) react with the acetic acid (CH₃COOH) to form water (H₂O) and acetate ions (CH₃COO⁻). This reaction consumes the added OH⁻ ions, preventing a significant increase in pH.
OH⁻(aq) + CH₃COOH(aq) ⇌ CH₃COO⁻(aq) + H₂O(l)
The Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation is a crucial tool for calculating the pH of a buffer solution and understanding its buffering capacity. For the acetic acid/sodium acetate buffer, the equation is:
pH = pKa + log([CH₃COO⁻]/[CH₃COOH])
Where:
- pH: The pH of the buffer solution.
- pKa: The negative logarithm of the acid dissociation constant (Ka) of acetic acid (approximately 4.76 at 25°C). The pKa represents the pH at which the concentrations of the acid and its conjugate base are equal.
- [CH₃COO⁻]: The concentration of acetate ions (from sodium acetate).
- [CH₃COOH]: The concentration of acetic acid.
This equation demonstrates that the pH of the buffer is determined by the ratio of the conjugate base concentration to the acid concentration. When this ratio is equal to 1, the pH equals the pKa.
Understanding the Logarithm Term
The logarithm term in the Henderson-Hasselbalch equation ([CH₃COO⁻]/[CH₃COOH]) indicates the buffer's effectiveness.
- When [CH₃COO⁻]/[CH₃COOH] > 1: The pH will be greater than the pKa, indicating a more alkaline buffer.
- When [CH₃COO⁻]/[CH₃COOH] < 1: The pH will be less than the pKa, indicating a more acidic buffer.
- When [CH₃COO⁻]/[CH₃COOH] = 1: The pH will equal the pKa, representing the buffer's optimal buffering capacity.
Buffering Capacity and Range
The buffering capacity refers to the amount of acid or base a buffer can neutralize before its pH changes significantly. The buffering capacity is highest when the concentrations of the acid and its conjugate base are approximately equal (i.e., when the pH is close to the pKa).
The buffering range is typically considered to be ±1 pH unit from the pKa. Outside this range, the buffer's capacity to resist pH changes diminishes considerably. For the acetic acid/sodium acetate buffer, the effective buffering range is approximately from pH 3.76 to 5.76.
Applications of the Acetic Acid/Sodium Acetate Buffer
The acetic acid/sodium acetate buffer finds numerous applications in various scientific fields, including:
- Biochemical experiments: Maintaining a stable pH in enzyme reactions, cell cultures, and other biological processes. The stable pH is crucial for optimal enzyme activity and cell viability.
- Analytical chemistry: Providing a constant pH environment for titrations and other analytical procedures. Accurate results depend on maintaining a consistent pH.
- Food preservation: Controlling the acidity of foods and beverages. Acetic acid, a component of vinegar, is already widely used for food preservation.
- Textile industry: In dyeing and finishing processes, where pH control is critical for colorfastness and fabric quality.
- Medical applications: Maintaining a specific pH in certain pharmaceutical preparations and drug delivery systems.
- Electroplating: Controlling the pH during electroplating processes, which significantly affects the quality of the coating.
Preparation of Acetic Acid/Sodium Acetate Buffer
Preparing an acetic acid/sodium acetate buffer involves calculating the required amounts of acetic acid and sodium acetate to achieve the desired pH. This often requires using the Henderson-Hasselbalch equation. For example, to prepare a buffer with a pH of 5.0:
-
Determine the desired pH and pKa: In this case, pH = 5.0, and pKa ≈ 4.76.
-
Use the Henderson-Hasselbalch equation:
5.0 = 4.76 + log([CH₃COO⁻]/[CH₃COOH]) -
Solve for the ratio of [CH₃COO⁻]/[CH₃COOH]:
log([CH₃COO⁻]/[CH₃COOH]) = 0.24 [CH₃COO⁻]/[CH₃COOH] = 10^0.24 ≈ 1.74 -
Choose the concentrations: You can choose any concentrations for acetic acid and sodium acetate, as long as their ratio is approximately 1.74. For example, you could use 0.1 M acetic acid and 0.174 M sodium acetate.
-
Calculate the required amounts: Based on the chosen concentrations and the desired buffer volume, you can calculate the amounts of acetic acid and sodium acetate needed. Remember to use appropriate molar masses and volumes.
Limitations and Considerations
While the acetic acid/sodium acetate buffer is versatile, it has limitations:
- Limited buffering range: Its effective range is limited to approximately pH 3.76 to 5.76. Outside this range, its buffering capacity significantly decreases.
- Temperature sensitivity: The pKa of acetic acid changes slightly with temperature, affecting the buffer's pH.
- Ionic strength: High ionic strength can alter the activity coefficients of the ions, affecting the calculated pH.
- Contamination: Contamination with strong acids or bases can significantly compromise the buffer's effectiveness.
Accurate preparation, careful handling, and awareness of its limitations are crucial for maximizing the effectiveness of the acetic acid/sodium acetate buffer in various applications.
Beyond the Basics: Exploring More Complex Scenarios
While the simple Henderson-Hasselbalch equation provides a good approximation for many situations, more complex calculations might be needed when considering factors like:
-
Activity coefficients: In solutions with high ionic strength, the activity of ions deviates from their concentration. Accurate calculations might require considering activity coefficients, which account for these deviations. The Debye-Hückel equation or its extensions can be used to estimate these activity coefficients.
-
Temperature effects: The pKa of acetic acid is temperature-dependent. For precise pH control at temperatures significantly different from 25°C, the temperature-dependent pKa value must be used in the Henderson-Hasselbalch equation. Experimental determination or literature values are often needed for this correction.
-
Mixing different buffer solutions: When combining buffer solutions with different concentrations or pH values, a more detailed calculation is needed to determine the final pH and buffering capacity of the resulting mixture. This often involves considering the equilibrium of all involved species and solving multiple simultaneous equations.
-
Buffer dilution: Diluting a buffer solution changes its concentration, which in turn affects its pH and buffering capacity. The Henderson-Hasselbalch equation can still be applied, but with the adjusted concentrations. However, very significant dilution may push the buffer beyond its effective range.
Understanding these complexities allows for more precise pH control and accurate predictions of buffer behavior in diverse experimental settings.
Conclusion
The acetic acid/sodium acetate buffer system is a fundamental concept in chemistry and biology. Its simplicity, readily available components, and relatively wide buffering range make it a valuable tool across diverse applications. A thorough understanding of the Henderson-Hasselbalch equation, the buffer's mechanism, and its limitations are crucial for its effective and safe use in scientific experiments, industrial processes, and other relevant fields. While the basic equation provides a useful approximation, considering more advanced concepts like activity coefficients and temperature effects will enhance the accuracy and precision of buffer calculations and applications in more complex scenarios.
Latest Posts
Latest Posts
-
Is Flammability A Physical Property Or Chemical Property
Apr 05, 2025
-
What Is The Five Carbon Sugar Found In Dna
Apr 05, 2025
-
Male Pine Cone Under Microscope Labeled
Apr 05, 2025
-
How Do I Multiply Rational Expressions
Apr 05, 2025
-
How Does A Competitive Inhibitor Slow Enzyme Catalysis
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Acetic Acid Sodium Acetate Buffer Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
