Electric Field Of Disk Of Charge
Muz Play
Mar 28, 2025 · 5 min read
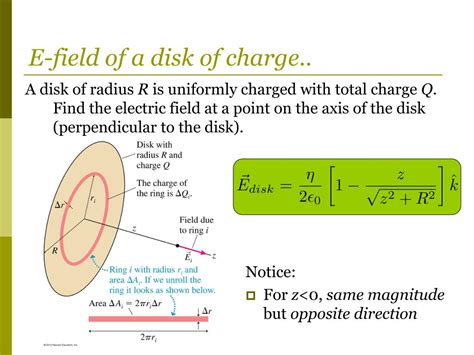
Table of Contents
Electric Field of a Disk of Charge: A Comprehensive Guide
The electric field, a fundamental concept in electromagnetism, describes the force exerted on a charged particle within its vicinity. Calculating the electric field for various charge distributions is crucial in understanding numerous physical phenomena. This article delves into the detailed calculation and analysis of the electric field produced by a uniformly charged disk. We'll explore different approaches, consider boundary conditions, and discuss the implications of this model in various applications.
Understanding the Problem: A Uniformly Charged Disk
Before diving into the calculations, let's clearly define our system. We're considering a thin, circular disk of radius R carrying a total charge Q uniformly distributed across its surface. Our goal is to determine the electric field at a point P located along the axis of symmetry, at a distance z from the center of the disk. We'll assume the disk is in vacuum, simplifying the calculations by eliminating the effects of permittivity.
Method 1: Integrating the Contribution from Each Charge Element
This is the most fundamental approach. We divide the disk into infinitesimally small charge elements, dQ. Each element contributes to the electric field at point P. We then integrate over the entire disk to find the total electric field.
1. Defining the Charge Element
Consider a thin ring of radius r and width dr within the disk. The area of this ring is dA = 2πr dr. Since the charge is uniformly distributed, the charge density (charge per unit area) is σ = Q/πR². Therefore, the charge on this ring is:
dQ = σ dA = (Q/πR²) * 2πr dr = (2Q/R²) * r dr
2. Calculating the Electric Field from a Ring Element
The electric field dE due to this ring element at point P is directed along the axis of symmetry (the z-axis). The components of dE perpendicular to the z-axis cancel out due to symmetry. The z-component of dE is:
dE<sub>z</sub> = k * dQ * cosθ / (r² + z²) = k * (2Q/R²) * r dr * z / [(r² + z²)<sup>3/2</sup>]
where k is Coulomb's constant (k = 1/(4πε₀)).
3. Integrating to Find the Total Electric Field
To find the total electric field, we integrate dE<sub>z</sub> over the entire disk (from r = 0 to r = R):
E<sub>z</sub> = ∫ dE<sub>z</sub> = ∫<sub>0</sub><sup>R</sup> k * (2Q/R²) * r dr * z / [(r² + z²)<sup>3/2</sup>]
This integral can be solved using substitution (let u = r² + z²). The result is:
*E<sub>z</sub> = kQz/R² * [1 - z/(√(R² + z²))] *
This is the final expression for the electric field along the axis of symmetry of a uniformly charged disk.
Method 2: Using Gauss's Law (for a specific case)
While Gauss's Law is generally powerful, its direct application to this problem isn't straightforward due to the lack of symmetry that easily allows construction of a Gaussian surface. However, we can use Gauss's law to address a limiting case: the electric field very far from the disk (z >> R).
In this limit, the disk appears as a point charge. Gauss's law states that the flux through a closed surface is proportional to the enclosed charge:
∮ E ⋅ dA = Q/ε₀
If we consider a large sphere centered on the disk, far away, the electric field is approximately radial and uniform over the sphere's surface. Thus:
E * 4πz² ≈ Q/ε₀
Therefore:
E ≈ Q/(4πε₀z²) = kQ/z²
This result is consistent with Coulomb's law for a point charge.
Analyzing the Result: Implications and Special Cases
The electric field expression *E<sub>z</sub> = kQz/R² * [1 - z/(√(R² + z²))] * provides valuable insights:
-
At the center of the disk (z = 0): E<sub>z</sub> = 0. This is expected due to symmetry. The contributions from opposite charge elements cancel each other out.
-
Very close to the disk (z << R): The expression simplifies to E<sub>z</sub> ≈ 2πkσ = σ/(2ε₀). The electric field is approximately uniform and independent of the distance. This resembles the electric field near an infinite sheet of charge.
-
Far from the disk (z >> R): The expression approaches E<sub>z</sub> ≈ kQ/z², which is the electric field of a point charge located at the center of the disk.
Applications and Extensions
The model of a uniformly charged disk has applications in various fields:
-
Modeling charged particles: A disk can approximate the charge distribution of a thin, circular object.
-
Electrostatic lenses: Uniformly charged disks are used to focus charged particle beams in scientific instruments.
-
Capacitors: Parallel plates of capacitors can be viewed as two disks facing each other. The electric field between the plates is essential for understanding the capacitor's behaviour.
-
Antenna design: The radiation pattern of an antenna can be modeled and analyzed using the electric field generated by a charged disk.
Beyond the Uniform Disk: Non-Uniform Charge Distributions
The calculation presented above assumed a uniform charge distribution. However, many real-world scenarios involve non-uniform charge distributions. Solving for the electric field in such cases requires more complex integration techniques, potentially involving numerical methods for complex charge densities.
For example, if the charge density is a function of the radial distance from the center (σ(r)), the integral for the electric field becomes:
E<sub>z</sub> = ∫<sub>0</sub><sup>R</sup> k * 2πr dr * σ(r) * z / [(r² + z²)<sup>3/2</sup>]
The specific solution depends entirely on the form of σ(r).
Conclusion
The electric field of a uniformly charged disk is a classic problem in electrostatics. Understanding its solution, obtained through integration or in limiting cases through Gauss's Law, provides a fundamental understanding of electric field calculations and the behavior of continuous charge distributions. The simplified model serves as a stepping stone for tackling more complex charge distributions and real-world problems where the disk model provides a reasonable approximation. The applications span various scientific and engineering disciplines, highlighting the importance of mastering this fundamental concept. This detailed analysis offers a comprehensive approach to understanding this important topic in electromagnetism, providing a solid foundation for further exploration of more advanced concepts.
Latest Posts
Latest Posts
-
Identifying The Important Intermolecular Forces In Pure Compounds
Mar 31, 2025
-
Why Does Km Increase In Competitive Inhibition
Mar 31, 2025
-
What Is The Electron Configuration Of Beryllium
Mar 31, 2025
-
When Do You Consider Log Diterminants Similar
Mar 31, 2025
-
Find The Rectangular Equation And Eliminate The Parameters
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of Disk Of Charge . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
