How Do You Square A Radical
Muz Play
Apr 02, 2025 · 5 min read
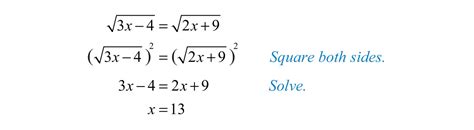
Table of Contents
How Do You Square a Radical? A Comprehensive Guide
Squaring a radical, or more accurately, squaring a radical expression, is a fundamental concept in algebra with wide-ranging applications. Understanding how to square radicals is crucial for simplifying expressions, solving equations, and tackling more advanced mathematical concepts. This comprehensive guide will break down the process step-by-step, covering various scenarios and providing ample examples to solidify your understanding.
Understanding Radicals and Squares
Before diving into the mechanics of squaring radicals, let's refresh our understanding of these core concepts.
What is a Radical?
A radical, symbolized by the radical symbol (√), represents a root of a number. The most common type is the square root, which indicates a number that, when multiplied by itself, yields the number under the radical sign (the radicand). For example:
- √9 = 3 because 3 * 3 = 9
- √16 = 4 because 4 * 4 = 16
Radicals can also represent cube roots (∛), fourth roots (∜), and so on, indicating the number that must be multiplied by itself that many times to equal the radicand.
What is Squaring?
Squaring a number means multiplying it by itself. For example:
- 3² = 3 * 3 = 9
- 5² = 5 * 5 = 25
- x² = x * x
Squaring Square Roots: The Fundamental Principle
The core principle behind squaring a radical is the inverse relationship between squaring and taking the square root. They essentially "undo" each other. Therefore, squaring a square root simplifies the expression significantly.
The Rule: (√a)² = a (where 'a' is a non-negative real number)
Example 1: Squaring a simple square root
(√25)² = 25
In this example, squaring the square root of 25 directly results in 25. The square root and the square operation cancel each other out.
Example 2: Squaring a square root with a variable
(√x)² = x (assuming x ≥ 0)
This principle works equally well with variables. Squaring the square root of 'x' gives you 'x' as long as x is a non-negative number. The reason for this restriction is that the square root is only defined for non-negative numbers in the real number system.
Squaring More Complex Radical Expressions
The process becomes slightly more involved when dealing with more complex radical expressions. However, the core principle remains the same.
Squaring Radicals with Coefficients
When a radical is multiplied by a coefficient, remember the order of operations (PEMDAS/BODMAS). Square the coefficient separately and then apply the principle for squaring the square root.
Example 3:
(3√7)² = 3² * (√7)² = 9 * 7 = 63
Here, we first squared the coefficient (3), resulting in 9. Then, we squared the square root of 7, which simplifies to 7. Finally, we multiply these results together.
Squaring Radicals with Variables Inside
When variables are present inside the radical, the same principles apply.
Example 4:
(√(4x))² = 4x (assuming x ≥ 0)
The square cancels out the square root, leaving us with the expression within the radical. Again, we need to ensure that the expression under the radical is non-negative to avoid issues with the square root definition.
Example 5:
(2√(5x²))² = 2² * (√(5x²))² = 4 * 5x² = 20x² (assuming x ≥ 0)
Here, we squared both the coefficient and the expression under the square root, then multiplied the results.
Squaring Radicals with Addition or Subtraction
Squaring radical expressions with addition or subtraction requires expanding the expression using the FOIL (First, Outer, Inner, Last) method.
Example 6:
(√2 + √3)² = (√2 + √3)(√2 + √3) = (√2)² + 2(√2)(√3) + (√3)² = 2 + 2√6 + 3 = 5 + 2√6
Notice that we cannot simply square each term individually; we must expand the expression to account for the cross-terms.
Example 7:
(√5 - √2)² = (√5 - √2)(√5 - √2) = (√5)² - 2(√5)(√2) + (√2)² = 5 - 2√10 + 2 = 7 - 2√10
Again, expanding using the FOIL method is essential.
Squaring Radicals with Fractions
Squaring radicals involving fractions requires careful attention to both the numerator and denominator.
Example 8:
(√(x/y))² = x/y (assuming x ≥ 0 and y > 0)
The square cancels the square root, leaving the fraction as is.
Applications of Squaring Radicals
Squaring radicals is a fundamental technique used in various mathematical contexts:
- Simplifying expressions: As demonstrated in the previous examples, squaring a radical can often significantly simplify an expression, making it easier to work with.
- Solving equations: Many equations involve radical expressions, and squaring both sides of the equation can be a crucial step in solving for the unknown variable. However, it is crucial to remember to check for extraneous solutions when squaring both sides of an equation as squaring can introduce extraneous solutions.
- Calculus: Squaring radicals is frequently used in calculus, especially when dealing with derivatives and integrals.
- Geometry: Many geometric formulas involve square roots, and squaring these radicals is often needed for calculations and problem-solving.
- Physics: Similar to geometry, many physical formulas involve radicals and require squaring for calculations and analysis.
Potential Pitfalls and Common Mistakes
While squaring radicals is a straightforward concept, some common mistakes can occur:
- Forgetting the order of operations: Always follow PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) to ensure correct calculations.
- Incorrectly squaring expressions with addition or subtraction: Remember to expand the expression using the FOIL method when squaring sums or differences of radicals.
- Not checking for extraneous solutions: When solving equations involving radicals by squaring both sides, always check your solutions in the original equation to eliminate any extraneous solutions.
- Neglecting restrictions on variables: Always consider the restrictions on variables to ensure that the radical is defined within the real number system (i.e., ensuring the expression inside the square root is non-negative).
Conclusion
Squaring a radical, especially a square root, is a critical skill in algebra and beyond. Understanding the fundamental principle of squaring canceling out the square root, coupled with a thorough grasp of the order of operations and the FOIL method, enables you to confidently handle even complex radical expressions. Remember to always double-check your work and be mindful of potential pitfalls. Mastering this skill will pave the way for a deeper understanding of more advanced mathematical concepts and their applications. By practicing the numerous examples provided and working through additional problems, you will solidify your understanding and become proficient in squaring radicals.
Latest Posts
Latest Posts
-
How Many Atoms Are In A Simple Cubic Unit Cell
Apr 03, 2025
-
Boiling Point Is A Chemical Property
Apr 03, 2025
-
Calculating Enthalpy Of Vaporization From Vapor Pressure
Apr 03, 2025
-
What Is The Solute In Salt Water
Apr 03, 2025
-
What Is Produced When An Acid Reacts With A Base
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Do You Square A Radical . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
