How To Balance A Nuclear Equation
Muz Play
Mar 26, 2025 · 6 min read
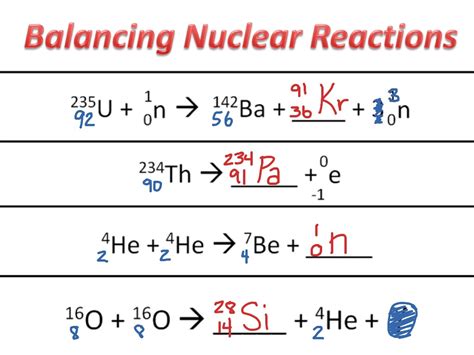
Table of Contents
How to Balance a Nuclear Equation: A Comprehensive Guide
Balancing nuclear equations might seem daunting at first, but with a systematic approach and a solid understanding of the fundamental principles, it becomes a manageable and even enjoyable process. This comprehensive guide will walk you through the intricacies of nuclear reactions, explaining the underlying concepts and providing step-by-step instructions for balancing various types of nuclear equations.
Understanding Nuclear Reactions: The Basics
Unlike chemical reactions which involve the rearrangement of atoms and electrons, nuclear reactions involve changes within the nucleus of an atom. These changes often result in the transformation of one element into another, accompanied by the release or absorption of enormous amounts of energy. Key concepts to grasp include:
1. Atomic Number (Z) and Mass Number (A)
- Atomic Number (Z): Represents the number of protons in the nucleus of an atom. It defines the element.
- Mass Number (A): Represents the total number of protons and neutrons in the nucleus.
These numbers are crucial for balancing nuclear equations. They are represented in the standard notation: ^A_Z X, where X is the element symbol. For example, ^235_{92}U represents Uranium-235, with 92 protons and 235 - 92 = 143 neutrons.
2. Types of Nuclear Reactions
Several types of nuclear reactions exist, each with its own characteristics:
- Alpha Decay (α-decay): An alpha particle (⁴₂He), consisting of two protons and two neutrons, is emitted from the nucleus.
- Beta Decay (β-decay): A neutron in the nucleus transforms into a proton, emitting an electron (β⁻) and an antineutrino (ν̅ₑ). There's also positron emission (β⁺-decay) where a proton transforms into a neutron, emitting a positron (β⁺) and a neutrino (νₑ).
- Gamma Decay (γ-decay): The nucleus releases energy in the form of a gamma ray (γ), a high-energy photon. This doesn't change the atomic or mass number.
- Neutron Emission (n): A neutron is ejected from the nucleus.
- Nuclear Fission: A heavy nucleus splits into two or more lighter nuclei, often releasing neutrons.
- Nuclear Fusion: Two light nuclei combine to form a heavier nucleus.
Understanding these reaction types is key to predicting the products and balancing the equation.
Balancing Nuclear Equations: A Step-by-Step Approach
The fundamental principle for balancing nuclear equations is the conservation of mass number (A) and atomic number (Z). This means the sum of A and Z on the reactant side must equal the sum of A and Z on the product side.
Here's a step-by-step approach:
Step 1: Identify the reactants and products. Carefully examine the given nuclear equation and identify all the reactants (on the left side) and products (on the right side).
Step 2: Write down the atomic and mass numbers for each species. This is crucial for tracking the conservation of A and Z.
Step 3: Apply the conservation laws. The sum of the mass numbers (A) on the reactant side must equal the sum of the mass numbers on the product side. Similarly, the sum of the atomic numbers (Z) on the reactant side must equal the sum of the atomic numbers on the product side.
Step 4: Solve for the unknown. If there's an unknown particle or element, use the conservation laws to solve for its atomic and mass numbers. This will allow you to identify the unknown species.
Step 5: Verify your solution. After you've found the unknown, double-check that the mass and atomic numbers are balanced on both sides of the equation.
Examples of Balancing Nuclear Equations
Let's illustrate this with several examples covering different types of nuclear reactions:
Example 1: Alpha Decay
Balance the following alpha decay equation:
^238_{92}U → ? + ^4_2He
Solution:
- Reactants:
^238_{92}U - Products:
^4_2Heand an unknown element (let's call it X) - Conservation of Mass Number (A): 238 = A + 4 => A = 234
- Conservation of Atomic Number (Z): 92 = Z + 2 => Z = 90
- Unknown Element: Element with Z = 90 is Thorium (Th).
- Balanced Equation:
^238_{92}U → ^234_{90}Th + ^4_2He
Example 2: Beta Decay
Balance the following beta decay equation:
^14_6C → ? + ^0_{-1}e + ν̅ₑ
Solution:
- Reactants:
^14_6C - Products:
^0_{-1}e(beta particle), antineutrino (ν̅ₑ), and an unknown element (X) - Conservation of Mass Number (A): 14 = A + 0 => A = 14
- Conservation of Atomic Number (Z): 6 = Z - 1 => Z = 7
- Unknown Element: Element with Z = 7 is Nitrogen (N).
- Balanced Equation:
^14_6C → ^14_7N + ^0_{-1}e + ν̅ₑ
Example 3: Nuclear Fission
Balance a simplified nuclear fission equation:
^235_{92}U + ^1_0n → ? + ^139_{56}Ba + 3^1_0n
Solution:
- Reactants:
^235_{92}Uand^1_0n - Products:
^139_{56}Ba,3^1_0n, and an unknown element (X) - Conservation of Mass Number (A): 235 + 1 = A + 139 + 3(1) => A = 94
- Conservation of Atomic Number (Z): 92 + 0 = Z + 56 + 0 => Z = 36
- Unknown Element: Element with Z = 36 is Krypton (Kr).
- Balanced Equation:
^235_{92}U + ^1_0n → ^94_{36}Kr + ^139_{56}Ba + 3^1_0n
Example 4: Nuclear Fusion
Balance the following nuclear fusion reaction:
^2_1H + ^3_1H → ? + ^1_0n
Solution:
- Reactants:
^2_1Hand^3_1H - Products:
^1_0nand an unknown element (X) - Conservation of Mass Number (A): 2 + 3 = A + 1 => A = 4
- Conservation of Atomic Number (Z): 1 + 1 = Z + 0 => Z = 2
- Unknown Element: Element with Z = 2 is Helium (He).
- Balanced Equation:
^2_1H + ^3_1H → ^4_2He + ^1_0n
Advanced Considerations and Challenges
While the basic principles remain consistent, balancing more complex nuclear equations can present challenges:
- Multiple Unknown Products: Some reactions might have more than one unknown product. You might need to use additional information, such as the type of decay or the known properties of the products.
- Isomeric States: Nuclei can exist in different energy states called isomers. These are represented by adding a superscript 'm' to the mass number (e.g.,
^99m_{43}Tc). Balancing equations involving isomers requires careful attention to the energy levels. - Complex Nuclear Fission: The fission of heavy nuclei can produce a wide range of products, making the balancing more complicated. Often, only the major products are considered for simplicity.
Conclusion
Balancing nuclear equations is a fundamental skill in nuclear chemistry and physics. By understanding the basic principles of conservation of mass number and atomic number, and by systematically applying the step-by-step approach, you can confidently tackle various types of nuclear equations, from simple alpha and beta decays to more complex fission and fusion reactions. Remember to always double-check your work to ensure the conservation laws are satisfied. With practice, balancing nuclear equations will become a routine and essential part of your understanding of nuclear processes. This thorough understanding will serve as a foundation for further exploration into the fascinating world of nuclear physics and chemistry.
Latest Posts
Latest Posts
-
How Temperature Affects The Rate Of Diffusion
Mar 29, 2025
-
Bobbie Gentry Ode To Billy Joe Lyrics
Mar 29, 2025
-
Chemical Families In The Periodic Table
Mar 29, 2025
-
A Disaccharide Is Formed By The Chemical Bonding Of
Mar 29, 2025
-
Electrolysis Is When Chemicals Break Down Into Charged Particles Called
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How To Balance A Nuclear Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
