How To Get Velocity From Flow Rate
Muz Play
Mar 28, 2025 · 6 min read
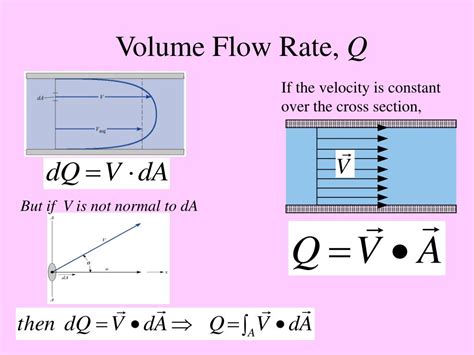
Table of Contents
How to Get Velocity from Flow Rate: A Comprehensive Guide
Understanding the relationship between flow rate and velocity is crucial in various fields, from fluid mechanics and hydraulic engineering to chemical processing and environmental science. While seemingly simple, the nuances of this relationship can be easily misunderstood, leading to inaccurate calculations and potentially serious consequences. This comprehensive guide will delve deep into the methods of calculating velocity from flow rate, exploring different scenarios and providing practical examples to solidify your understanding.
Understanding the Fundamentals: Flow Rate vs. Velocity
Before we dive into the calculations, let's clarify the definitions of our key terms:
-
Flow Rate (Q): This refers to the volume of fluid passing a given point per unit of time. It's typically expressed in units like cubic meters per second (m³/s), liters per minute (L/min), or gallons per minute (GPM). Flow rate represents the overall movement of the fluid.
-
Velocity (v): This is a vector quantity representing the speed and direction of fluid movement at a specific point within the flow. It's typically expressed in units like meters per second (m/s), feet per second (ft/s), or kilometers per hour (km/h). Velocity describes the local motion of the fluid.
The critical distinction is that flow rate describes the total fluid movement, while velocity describes the fluid's movement at a particular location. They are related but not interchangeable.
Calculating Velocity from Flow Rate: The Simple Case (Uniform Flow in a Pipe)
The simplest scenario involves calculating the velocity of fluid in a pipe with a uniform cross-sectional area. In this case, the relationship is straightforward:
v = Q / A
Where:
- v is the average velocity of the fluid.
- Q is the volumetric flow rate.
- A is the cross-sectional area of the pipe.
Example:
Let's say we have a pipe with a diameter of 10 cm (0.1 m) carrying water at a flow rate of 0.1 m³/s. To find the average velocity:
-
Calculate the cross-sectional area: A = πr² = π(0.05 m)² ≈ 0.00785 m²
-
Calculate the velocity: v = 0.1 m³/s / 0.00785 m² ≈ 12.73 m/s
Therefore, the average velocity of the water in the pipe is approximately 12.73 m/s.
Important Considerations:
-
Uniform Flow: This formula assumes a uniform flow profile, meaning the velocity is constant across the entire cross-sectional area. In reality, this is rarely perfectly achieved due to factors like friction at the pipe walls. The calculated velocity is an average velocity.
-
Laminar vs. Turbulent Flow: The nature of the flow (laminar or turbulent) affects the accuracy of this calculation. In turbulent flow, the velocity profile is more complex, and the average velocity might not accurately represent the local velocities.
-
Units: Always ensure consistent units throughout your calculations. Inconsistencies can lead to significant errors.
Calculating Velocity in More Complex Scenarios
The simple formula above only applies to uniform flow in a pipe with a constant cross-sectional area. In many real-world situations, the flow is far more complex. Let's explore some common scenarios:
1. Non-Uniform Flow in Pipes
When the pipe diameter changes, the velocity changes as well. The principle of conservation of mass dictates that the flow rate (Q) remains constant along the pipe, even if the cross-sectional area changes. Therefore, we can use the continuity equation:
Q = A₁v₁ = A₂v₂
Where:
- A₁ and A₂ are the cross-sectional areas at two different points in the pipe.
- v₁ and v₂ are the velocities at those two points.
This equation allows you to calculate the velocity at one point if you know the velocity and area at another point.
2. Open Channels
Calculating velocity in open channels is more complex than in closed pipes. The flow is often influenced by factors like channel geometry, slope, roughness, and the depth of the water. Empirical formulas, such as Manning's equation or Chezy's formula, are commonly used to estimate the velocity. These formulas incorporate factors like the hydraulic radius and the channel's roughness coefficient.
Manning's Equation (Example):
v = (1/n) * R^(2/3) * S^(1/2)
Where:
- v is the average velocity.
- n is the Manning's roughness coefficient (depends on the channel material).
- R is the hydraulic radius (cross-sectional area divided by the wetted perimeter).
- S is the channel slope.
3. Flow in Irregular Geometries
For flows in irregularly shaped channels or conduits, numerical methods, such as computational fluid dynamics (CFD), are often necessary to accurately determine the velocity profile. CFD simulations solve the Navier-Stokes equations to model the fluid flow, providing detailed velocity information throughout the flow domain.
Practical Applications and Real-World Examples
Understanding how to determine velocity from flow rate has numerous practical applications:
-
Hydraulic Engineering: Designing and analyzing water distribution systems, dams, canals, and other hydraulic structures requires accurate velocity calculations to ensure efficient flow and prevent erosion or flooding.
-
Chemical Engineering: In chemical processes, precise control over fluid flow and velocity is crucial for efficient mixing, reaction rates, and heat transfer.
-
Environmental Engineering: Modeling water flow in rivers and streams is vital for assessing water quality, pollutant transport, and ecological impacts. Velocity measurements are crucial for understanding these processes.
-
Aerospace Engineering: Understanding airflow over aircraft wings and other aerodynamic surfaces is essential for designing efficient and stable vehicles. Velocity calculations are fundamental to this process.
-
Medical Applications: In medical devices and procedures involving fluid flow, accurate velocity measurements are crucial for ensuring proper functioning and patient safety.
Advanced Considerations and Error Analysis
Several factors can affect the accuracy of velocity calculations:
-
Measurement Errors: Inaccurate measurements of flow rate or cross-sectional area can lead to significant errors in the calculated velocity. Calibration and careful measurement techniques are essential.
-
Non-uniform Velocity Profiles: As mentioned earlier, the assumption of uniform velocity is often inaccurate. Real-world flows often exhibit complex velocity profiles, making average velocity calculations less precise.
-
Friction Losses: Friction between the fluid and the pipe walls or channel boundaries causes energy losses and affects the velocity. Accounting for these losses is crucial for accurate calculations, particularly in longer pipes or channels.
-
Compressibility: The calculations discussed above assume incompressible flow. For high-velocity flows or flows involving gases, compressibility effects can become significant and need to be considered.
Properly accounting for these factors and employing appropriate error analysis techniques is crucial for ensuring the reliability of velocity calculations.
Conclusion
Calculating velocity from flow rate is a fundamental concept in fluid mechanics with widespread applications. While the simple formula (v = Q/A) provides a useful starting point, understanding the limitations and employing more sophisticated techniques for complex scenarios is essential for obtaining accurate and reliable results. The choice of method depends heavily on the specific application and the complexity of the flow. Always remember to carefully consider the assumptions made and the potential sources of error in your calculations. With careful attention to detail and a solid understanding of the underlying principles, you can confidently determine velocity from flow rate in various applications.
Latest Posts
Latest Posts
-
Integrals Of Even And Odd Functions
Mar 31, 2025
-
What Makes Something A Strong Acid
Mar 31, 2025
-
According To The Rules Of Osmosis A System Will
Mar 31, 2025
-
Where Are Chondrocytes And Osteocytes Located
Mar 31, 2025
-
List The Types Of Persuasive Speeches
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Get Velocity From Flow Rate . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
