Kinetic And Potential Energy In A Pendulum
Muz Play
Mar 28, 2025 · 6 min read
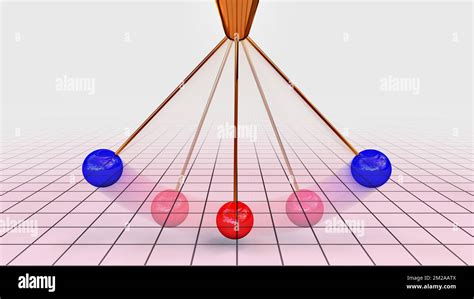
Table of Contents
Kinetic and Potential Energy in a Pendulum: A Deep Dive
The simple pendulum, a seemingly basic system consisting of a mass suspended from a fixed point by a string or rod, provides a fascinating illustration of the interplay between kinetic and potential energy. Understanding this interplay is crucial not only for grasping fundamental physics concepts but also for applications ranging from clock mechanisms to sophisticated engineering designs. This article delves into the intricate dance of kinetic and potential energy within a pendulum, exploring its mechanics, variations, and real-world implications.
Understanding Kinetic and Potential Energy
Before examining the pendulum's behavior, let's establish a firm understanding of the two key forms of energy involved:
Kinetic Energy: The Energy of Motion
Kinetic energy (KE) is the energy possessed by an object due to its motion. The faster an object moves, the greater its kinetic energy. Quantitatively, kinetic energy is expressed as:
KE = ½ * m * v²
Where:
- m represents the mass of the object (in kilograms).
- v represents the velocity of the object (in meters per second).
In simpler terms, a heavier object moving at a given speed possesses more kinetic energy than a lighter object moving at the same speed. Similarly, an object moving at a higher speed has more kinetic energy than the same object moving slower.
Potential Energy: The Energy of Position
Potential energy (PE), on the other hand, is the energy stored within an object due to its position or configuration. In the case of a pendulum, we're primarily concerned with gravitational potential energy (GPE), which is the energy stored due to an object's position relative to a gravitational field. The higher an object is lifted against gravity, the greater its gravitational potential energy. The formula for gravitational potential energy is:
PE = m * g * h
Where:
- m represents the mass of the object (in kilograms).
- g represents the acceleration due to gravity (approximately 9.8 m/s² on Earth).
- h represents the height of the object above a reference point (in meters).
The Pendulum's Energy Transformation
The beauty of the simple pendulum lies in its continuous conversion between kinetic and potential energy. Let's trace this transformation throughout a single oscillation:
-
Maximum Potential Energy, Zero Kinetic Energy: At the highest point of its swing (the amplitude), the pendulum momentarily stops. At this point, its velocity is zero, meaning its kinetic energy is also zero. However, because it is at its highest point, it possesses maximum gravitational potential energy. All the energy is stored as potential energy.
-
Energy Conversion Begins: As the pendulum begins its descent, its potential energy starts converting into kinetic energy. Gravity accelerates the mass, increasing its velocity.
-
Maximum Kinetic Energy, Zero Potential Energy: At the pendulum's lowest point (equilibrium position), its height is minimal (often considered zero). At this point, all the potential energy has been transformed into kinetic energy. The pendulum is moving at its maximum velocity, possessing maximum kinetic energy and zero potential energy (relative to the lowest point).
-
Energy Conversion Reverses: As the pendulum continues its swing upward, it slows down. Its kinetic energy is now converted back into potential energy. The velocity decreases, and the height increases.
-
The Cycle Repeats: This cycle of energy conversion continues as the pendulum swings back and forth. In an ideal pendulum (without friction or air resistance), this energy transformation would continue indefinitely, with the total mechanical energy (the sum of kinetic and potential energy) remaining constant.
Factors Affecting Pendulum Motion
Several factors influence the motion and energy transformations of a pendulum:
1. Mass:
The mass of the pendulum bob affects both its kinetic and potential energy. A heavier bob will possess more kinetic energy at a given velocity and more potential energy at a given height. However, the period of the pendulum (the time it takes for one complete oscillation) remains unaffected by the mass (assuming a massless string/rod). This is a key characteristic of simple pendulums.
2. Length:
The length of the pendulum string or rod significantly impacts its period. Longer pendulums have longer periods, swinging more slowly. The length also influences the maximum height the bob reaches, thus affecting the maximum potential energy.
3. Amplitude:
The amplitude, or maximum angle of displacement from the equilibrium position, influences the maximum potential energy. A larger amplitude means a greater height and therefore greater potential energy at the highest point. However, for small amplitudes (less than about 15 degrees), the pendulum's period remains relatively constant, independent of the amplitude. This is a crucial approximation used in many calculations.
4. Gravity:
The acceleration due to gravity directly influences the potential energy and the rate at which the pendulum converts between kinetic and potential energy. A stronger gravitational field will result in faster oscillations and a greater rate of energy conversion. On different celestial bodies with varying gravitational accelerations, pendulum periods would change accordingly.
5. Damping Forces (Friction and Air Resistance):
In a real-world scenario, damping forces like friction and air resistance play a significant role. These forces dissipate energy, causing the pendulum's oscillations to gradually decrease in amplitude until it comes to rest. The total mechanical energy is not conserved in the presence of damping forces. The lost mechanical energy is converted into thermal energy (heat).
Real-World Applications
The principles of kinetic and potential energy in a pendulum have far-reaching practical applications:
-
Clocks: Early mechanical clocks utilized the consistent period of a pendulum to regulate timekeeping. The pendulum's regular back-and-forth motion provided a reliable mechanism for measuring time.
-
Seismic Sensors: The sensitivity of a pendulum to even slight changes in its environment makes it a useful component in seismometers, instruments used to detect and measure earthquakes.
-
Metronomes: Metronomes use a pendulum to maintain a consistent tempo for musicians, helping them maintain a steady rhythm.
-
Engineering Designs: The pendulum's energy conversion principles are used in designing various mechanical systems, including some types of oscillators and vibration dampeners. Understanding the energy transfer is critical in designing effective and efficient systems.
Beyond the Simple Pendulum: Complex Systems
While the simple pendulum provides a foundational understanding of kinetic and potential energy interplay, many real-world systems involve more complex pendulums. These include:
-
Compound Pendulum: This involves a rigid body swinging about a fixed pivot point. The calculation of the period is more complex than for the simple pendulum, requiring the consideration of the body's moment of inertia.
-
Double Pendulum: This system consists of two pendulums connected in series, exhibiting chaotic motion and complex energy transformations. The energy exchange is far more intricate and difficult to predict precisely.
-
Damped Pendulum: The inclusion of damping forces, such as air resistance and friction, leads to a gradual decay of oscillations and loss of mechanical energy.
Conclusion
The simple pendulum, despite its apparent simplicity, offers a profound illustration of the fundamental principles of kinetic and potential energy. The continuous conversion between these forms of energy, governed by gravity and influenced by various factors, creates a fascinating and widely applicable system. From precise timekeeping to sensitive earthquake detection, understanding the dynamics of energy in a pendulum is critical for various scientific and engineering advancements. The study of pendulums extends beyond the simple model, opening doors to more complex systems exhibiting chaotic behaviour and highlighting the rich interplay of energy in the physical world. Further exploration of damped pendulums, compound pendulums, and even coupled pendulum systems allows for a deeper understanding of energy conservation and dissipation, ultimately advancing our knowledge of classical mechanics.
Latest Posts
Latest Posts
-
Why Do Plants Love Water In Bio Terms
Mar 31, 2025
-
Identifying The Important Intermolecular Forces In Pure Compounds
Mar 31, 2025
-
Why Does Km Increase In Competitive Inhibition
Mar 31, 2025
-
What Is The Electron Configuration Of Beryllium
Mar 31, 2025
-
When Do You Consider Log Diterminants Similar
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Kinetic And Potential Energy In A Pendulum . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
