Relation Between Electric Field And Electric Potential
Muz Play
Mar 28, 2025 · 7 min read
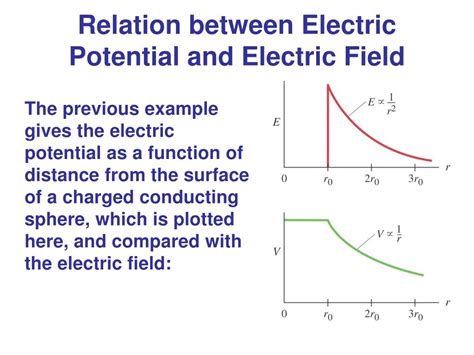
Table of Contents
The Intimate Dance of Electric Field and Electric Potential: A Deep Dive
The seemingly invisible forces governing electricity are elegantly described by two fundamental concepts: the electric field and the electric potential. While distinct, these concepts are inextricably linked, forming a powerful duo that explains a vast range of electrical phenomena, from the simple attraction between charged particles to the complex workings of modern electronics. This article delves deep into the relationship between these two crucial concepts, exploring their definitions, their mathematical connection, and their practical applications.
Understanding the Electric Field: A Force Field in Action
Imagine a point charge, a tiny speck of concentrated electric charge. This charge exerts a force on any other charged particle brought into its vicinity. This force is not some mystical action at a distance; instead, it's mediated by the electric field, a vector field that permeates the space surrounding the charge.
The electric field at any point in space is defined as the force per unit charge experienced by a small positive test charge placed at that point. Mathematically, it's represented as:
E = F/q
where:
- E represents the electric field vector (units: Newtons per Coulomb, N/C or Volts per meter, V/m)
- F is the electric force vector (units: Newtons, N)
- q is the magnitude of the test charge (units: Coulombs, C)
It's crucial to note that the electric field is independent of the test charge. The field itself is a property of the source charge(s) creating it. The test charge simply allows us to measure the field's strength and direction at a specific point.
Visualizing the Electric Field: Field Lines
Electric field lines are a powerful visual tool to represent the electric field. These lines originate from positive charges and terminate on negative charges. The density of the lines indicates the field's strength – a higher density implies a stronger field. The direction of the lines at any point indicates the direction of the force a positive test charge would experience if placed there.
For example, the electric field lines around a single positive point charge radiate outwards, indicating that the field points away from the charge. For a pair of opposite charges (a dipole), the field lines originate from the positive charge and curve towards the negative charge, illustrating the attractive force between them.
Calculating Electric Fields: From Point Charges to Complex Systems
Calculating electric fields can range from simple to extremely complex. For a point charge, Coulomb's Law provides a straightforward calculation:
E = kQ/r²
where:
- k is Coulomb's constant (approximately 8.99 x 10⁹ N⋅m²/C²)
- Q is the magnitude of the source charge
- r is the distance from the source charge to the point where the field is being calculated.
For more complex charge distributions, such as continuous charge distributions (lines, surfaces, or volumes), integration techniques are required to sum up the contributions of infinitesimal charge elements. This often involves sophisticated vector calculus. However, the underlying principle remains consistent: the electric field at a point is the vector sum of the fields produced by each individual charge element.
Unveiling Electric Potential: Energy Landscape of Charge
While the electric field describes the force experienced by a charge, the electric potential (often simply called potential) describes the potential energy per unit charge at a given point in the electric field. It's a scalar quantity, meaning it has magnitude but no direction, unlike the vector electric field.
The electric potential (V) at a point is defined as the work done per unit charge in moving a positive test charge from a reference point (often taken as infinity) to that point. This is expressed mathematically as:
V = W/q
where:
- V represents the electric potential (units: Volts, V)
- W is the work done (units: Joules, J)
- q is the magnitude of the test charge (units: Coulombs, C)
The potential difference between two points, often called the voltage, represents the work done per unit charge in moving a charge between those two points. This is what drives current in circuits.
Equipotential Surfaces: Contour Maps of Potential
Just as field lines help visualize the electric field, equipotential surfaces depict the electric potential. These are surfaces where the electric potential has a constant value. No work is done in moving a charge along an equipotential surface, as there is no change in potential energy.
Equipotential surfaces are always perpendicular to electric field lines. This is because if a charge were to move along a field line, it would experience a force and thus a change in potential energy. Conversely, movement along an equipotential surface results in no change in potential energy, hence the perpendicularity.
Calculating Electric Potential: From Point Charges to Continuous Distributions
Similar to electric field calculations, determining the electric potential can range in complexity. For a point charge, the potential at a distance r is given by:
V = kQ/r
Notice the inverse relationship with distance, contrasting with the inverse square relationship for the electric field. This means the potential decreases less rapidly with distance than the field strength.
For continuous charge distributions, integration techniques are once again necessary to sum the contributions from all charge elements.
The Intertwined Dance: Connecting Electric Field and Potential
The electric field and electric potential are intrinsically linked. They are not independent entities but rather two different mathematical descriptions of the same underlying physical phenomenon – the effect of electric charges on their surroundings.
The most crucial connection lies in the fact that the electric field is the negative gradient of the electric potential. In simpler terms, the electric field points in the direction of the steepest decrease in potential. Mathematically, this relationship is expressed as:
E = -∇V
where:
- ∇ is the del operator, a vector differential operator that calculates the gradient of a scalar function. In Cartesian coordinates, this becomes: ∇V = (∂V/∂x)î + (∂V/∂y)ĵ + (∂V/∂z)k̂
This equation is fundamental. It tells us that the electric field is directly related to the spatial variation of the electric potential. Where the potential changes rapidly, the electric field is strong. Where the potential is relatively constant (like on an equipotential surface), the electric field is weak or zero.
Conversely, the electric potential can be calculated by integrating the electric field along a path:
V(b) - V(a) = -∫<sub>a</sub><sup>b</sup> E ⋅ dl
This equation states that the potential difference between two points is the negative line integral of the electric field along any path connecting the two points. The path independence of this integral reflects the conservative nature of the electrostatic field.
Applications: From Everyday Devices to Cutting-Edge Technology
The relationship between electric field and electric potential isn't just an academic exercise; it underpins countless technologies and phenomena in our daily lives:
-
Capacitors: These devices store electrical energy by accumulating charge on two conductive plates separated by an insulator. The electric field between the plates is directly related to the voltage (potential difference) across them, and the stored energy is directly proportional to the square of the voltage.
-
Batteries: Batteries provide a potential difference (voltage) that drives the flow of current through a circuit. This voltage is a manifestation of the chemical potential energy difference between the battery's electrodes, resulting in an electric field within the battery and the external circuit.
-
Electrostatic Discharge (ESD): ESD occurs when a rapid discharge of static electricity occurs, often causing damage to sensitive electronic components. The discharge is driven by a large potential difference between objects, leading to a strong electric field that can cause significant damage.
-
Medical Imaging: Techniques like electrocardiography (ECG) and electroencephalography (EEG) measure the potential differences generated by the electrical activity of the heart and brain, respectively. These potential differences are indicative of the underlying electric fields and are invaluable for diagnosing various medical conditions.
-
Particle Accelerators: These devices use powerful electric fields to accelerate charged particles to incredibly high speeds. The electric field provides the force, while the potential difference dictates the energy gained by the particles.
Conclusion: A Unified View of Electrical Phenomena
The relationship between electric field and electric potential is a cornerstone of electromagnetism. Understanding this connection provides a unified and powerful framework for analyzing and predicting a wide range of electrical phenomena. From the simple attraction of charged particles to the intricate workings of modern electronics, these two concepts are essential for comprehending the world of electricity. While distinct in their nature – one a vector field describing force, the other a scalar field describing potential energy – their intimate mathematical connection reveals the profound elegance and unity of physical laws. The interplay between these forces is a testament to the underlying simplicity and beauty of the universe's fundamental interactions.
Latest Posts
Latest Posts
-
How Is Energy Involved In Chemical And Physical Changes
Mar 31, 2025
-
What Happens When You Combine An Acid And A Base
Mar 31, 2025
-
How To Solve A Rational Exponent
Mar 31, 2025
-
Heat Of Combustion Of Benzoic Acid
Mar 31, 2025
-
How To Round Sig Figs When Adding
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Relation Between Electric Field And Electric Potential . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
